Compressional Waves
Michael Fowler, UVa
Balls and Springs
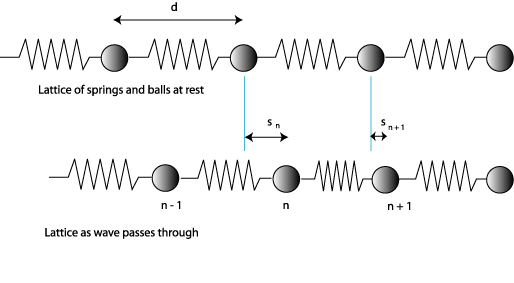
To understand the mechanics of a compressional wave moving through a solid, it is helpful to think about a simple one-dimensional model. Consider a “lattice” made up of balls, representing atoms, equally spaced distance d from the center of one atom to the center of the next (this distance is called the lattice constant) and joined by springs (representing atomic bonds) which obey Hooke’s law, with spring constant B/d, so that if the distance between two atoms is different from d the spring exerts a force on the two atoms of magnitude Bx/d, where x is the distance the spring is stretched (or compressed) away from its natural length.
(Side comment: The usual Hooke’s law spring constant is defined slightly differently from the bulk modulus! If a spring is stretched by x, the force the spring exerts is usually given by Hooke’s coefficient k multiplied by x: F = -kx. The actual unstretched length d of the spring doesn’t appear. However, the bulk modulus relates the force exerted to the relative length change, DV/V or for a chain DL/L. Since our aim here is to build a solid, with a bulk modulus, from balls and springs, we have to begin with springs whose elastic properties are already given in terms of a “bulk modulus”—that is, are defined in terms of relative length change DL/L, or x/d, not just the stretch x, and that is why we write F = -Bx/d.)
So, when the lattice is at rest, the distance between atom centers is d, and the springs are exerting zero force on the atoms. (We neglect here any vibrations caused by heat.) Now suppose a wave passes through, and at some moment as the wave passes the atoms are away from their rest positions—the nth atom being displaced a distance sn to the right from rest. Obviously, these variables sn are varying in time.
Applying F = ma to One Atom
To find how the atoms move, we apply Newton’s Law F = ma to one atom. The forces the nth atom feels are from the two springs connecting it to its neighbors. If the nth atom is displaced to the right by sn, and the n + 1 th atom by sn + 1, then the spring between the two is being stretched by sn + 1 – sn beyond its natural length, and therefore is pulling the nth atom to the right with a force B(sn + 1 – sn)/d. (Of course, if sn + 1 is less than sn, the spring is compressed, and it pushes the nth atom to the left. This possibility is automatically taken care of, because the sign of sn + 1 – sn will change.) There is a corresponding force from the other spring, so putting them together:
![]()
We have one equation like this for each atom. But, with millions of atoms, how can we solve them?
From Millions of Equations to One
The key to solving all these equations is to realize that for the sound waves we are interested in, the wavelength of the wave, the distance over which the sn’s vary, is vastly greater than the distance d between the atoms. This means the difference between sn and sn + 1 is very tiny. Therefore, if we plot the sn’s on a graph, pointing them upwards so we can see them, we can draw a very smooth, slowly varying curve through them.

That is to say,
s(x,t) =sn(t) for x = nd.
We can take advantage of the very slow rate of change of s(x,t) on an atomic scale to write the difference of neighboring displacements as the derivative of s(x,t).
That is, the relative extension (or compression) DL/L of the spring is given by:
![]()
to an excellent approximation.
But we can take one further step: applying the same analysis to the term from the other spring in the Newton’s Law equation gives
![]()
and adding these two terms
![]()
Using this to replace the difference terms on the right hand side of the Newton’s Law equation (and noting that m/d is the mass per unit length r) gives:
![]()
To summarize: applying F = ma to the horizontal displacement motion of the atoms in a ball and springs model, and making the assumption that the relevant wavelength is much greater than the distance between atoms, so that we can replace differences by derivatives, we have derived the wave equation
![]()
This is identical to the wave equation derived for transverse waves on a string, except that now the elastic modulus B plays the role of the tension T in the string. Since it is the same equation, it has the same solutions: any (differentiable) function of the form f(x- ct) or f(x + ct).
Going to Three Dimensions
Actually, our toy model with balls and springs is easily adapted to explain how sound waves travel down a metal bar, for example, hit by a hammer at one end. If we assume the hammer hits flat against the end, we can imagine the metal bar divided into thin slices, like sliced bread, and as the compression wave travels down, the nth slice is displaced sn(t) from its rest position. In fact, the atoms in a crystalline material (for example a metal) are arranged in planes, held in place by spring-like chemical bonds, a three dimensional generalization of our balls and springs, so even on an atomic level our picture is not far from the truth.
Things are a little different, however, for a sound wave in a gas, like air. As we shall discuss in much more detail later, the air molecules are not connected to each other by springs, in fact they are flying about at speeds of hundreds of meters per second, frequently colliding with each other, so the balls and springs model seems irrelevant.
The key to understanding how a sound wave can travel through a gas is to realize that the wavelength is far greater than the microscopic length scale defined by the distance between atoms, or even between atomic collisions. The shortest wavelength sound anyone can hear has a wavelength around one centimeter, and we know from everyday experience that on this scale air behaves as a smooth continuous fluid, with a well-defined density of 1.29 kg/m3, and a bulk modulus B of about 1.5´105 Pa, where the bulk modulus is defined as the pressure change arising from an incremental change in volume,
![]()
Let us consider a sound wave propagating down a pipe. We do not pretend to analyze what’s going on at the molecular level, we treat the air as a continuous fluid. We imagine the air in the pipe as made up of slices, the slices being much thinner than the wavelength of the sound traveling through, and hence a lot thinner than those shown below.
. 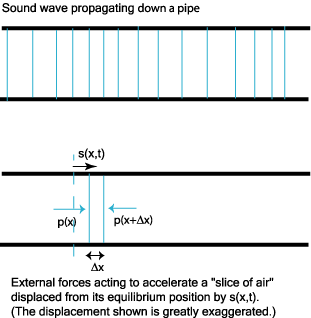
Once again, we apply Newton’s law F = ma to an element of the system, in this case a thin slice of air. As the sound wave passes, this slice moves backwards and forwards, its position at time t being s(x,t) away from its equilibrium position x.
If the tube has cross-section area A, the slice of air has volume ADx and mass ADxr. The force acting on it causing it to accelerate is the pressure difference between the two sides, multiplied by the area A the pressure acts on.
To find the F in F = ma, we need to know the pressure at the points x and x + Dx in the gas: to be precise, the difference from the surrounding atmospheric pressure. This extra pressure arises because the gas is compressed or expanded from its equilibrium density, just like the spring force in the balls and springs model. And, in exact parallel to that case, the differential volume change is the derivative of the displacement function: DV/V = -¶s(x,t)/¶x.
Therefore, the extra pressure at x,
![]()
and the net force on the slice of air,
![]() .
.
Putting this equal to the mass of the slice of air ADxr times its acceleration ¶2s/¶t2, gives again:
![]()
Ó 2002 Michael Fowler